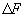 gilt für eine Menge B
die eine nichtleere offene Kugel
gilt für eine Menge B
die eine nichtleere offene Kugel 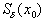 um einen Punkt
um einen Punkt
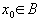 enthält:
enthält:
[<] [globale Übersicht] [Kapitelübersicht] [Stichwortsuche] [>]
Abschätzung der relativen Konditionszahlen linearer Probleme
Im folgenden werden relative Konditionszahlen linearerinverser
Probleme (z.B. linearer Gleichungssysteme) angegeben. Für lineare Operator
und 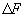 gilt für eine Menge B
die eine nichtleere offene Kugel
gilt für eine Menge B
die eine nichtleere offene Kugel 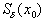 um einen Punkt
um einen Punkt
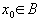 enthält:
enthält:
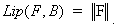 ,
,
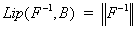 und
und 
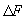 = 0); so erhält man
= 0); so erhält man
![\[
\| \Delta x \| \le \Lip(F^{-1},B) \| \Delta y \| =
\| F^{-1} \| \| \Delta y \|
\]](pic/b06_11aj.gif)
![\[
\| y \| = \| Fx \| \le \| F \| \| x \|
\]](pic/b06_12aj.gif)

Wenn nur Störungen der Funktion F berücksichtigt werden(
y bleibt ungestört, sodaß 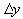 = 0 gilt)
erhält man
= 0 gilt)
erhält man
= =
und somit
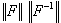 als Konditionszahl, wobei aber
der relative Fehler auf die gestörte Lösung
als Konditionszahl, wobei aber
der relative Fehler auf die gestörte Lösung 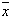 bezogen ist. Die analoge
Formel, bei der der relative Fehler auf x bezogen ist, folgt
mit
bezogen ist. Die analoge
Formel, bei der der relative Fehler auf x bezogen ist, folgt
mit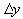 = 0:
= 0:
![\[ %\label{eqn:1.2-48}
\frac{\| \Delta x \|}{\| x \|} \le
\frac{\| F \| \| F^{-1} \|}{1 - \| F^{-1} \| \| \Delta F \|}
\frac{\| \Delta F \|}{\| F \|}.
\]](pic/b06_18aj.gif)
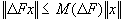 und
und 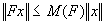
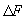 im betrachteten Gebiet B "ähnlich" linearen Abbildungen verhalten
im betrachteten Gebiet B "ähnlich" linearen Abbildungen verhalten