Kerschhofer
[ < ]
[ globale Übersicht ]
[ Kapitelübersicht ]
[ Stichwortsuche ]
[ > ]
Das Newtonverfahren
Wir haben das Newtonverfahren bereits für die iterative
Lösung von nichtlinearen Gleichungen kennengelernt. Dieses Verfahren
kann auch nichtlineare Gleichungssysteme lösen. Dabei wird ganz analog
vorgegangen:
Zur Erinnerung: bei nichtlinearen Gleichungen wurde der Punkt x(k+1)
errechnet, indem an der Stelle x(k) eine Tangente an die Funktion gelegt
, und diese Tangente mit der x-Achse geschnitten wurde. Der Schnittpunkt
war an der gesuchten Stelle x(k+1). Die Tangente hat gemäß der Geradengleichung y = kx+d die
Gestalt
f(x) = f '(x) x + f(x) c
oder umgeformt
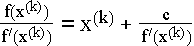
Der Punkt x(k+1) liegt auch auf dieser Geraden, und der Funktionswert
ist an dieser Stelle gleich 0.
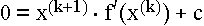
das bedeutet
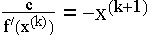
daraus ergibt sich die Iterationsvorschrift
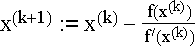
Beim Newtonverfahren für NLGS geht man äquivalent vor, und
die Iterationsvorschrift sieht folgendermaßen aus:
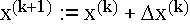
wobei gilt:
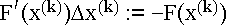
Man erkennt schon die Analogie, muß aber beachten:
-
es werden keine Nullstellen gesucht, sondern Schnittpunkte der (Hyper)
Ebenen
-
das x ist hier ein Vektor
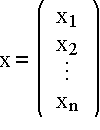
-
das gegebene Gleichungssystem steht in der Matrix F(x)
-
statt der ersten Ableitung wird die Jacobi- Matrix F'(x) verwendet
In der Praxis bedeutet das folgendes Vorgehen
-
Bestimmung eines geeigneten Startwertes
-
Bestimmung der Jacobi- Matrix
-
Einsetzen des (Start-) Vektors in
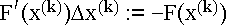 ,
das liefert ein lineares Gleichungssystem
,
das liefert ein lineares Gleichungssystem
-
Lösen des lin. Gls., das liefert den Vektor
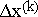
-
Fortsetzen bei Punkt 3
Rechenaufwand
Dieser wird hauptsächlich von Punkt 3 bestimmt. Einsetzen des
Vektors x(k) in die Jacobi- Matrix F'(x) hat den Aufwand n2. Einsetzen
des Vektors x(k) in F(x) hat den Aufwand n, macht zusammen n2 + n.
Für die Lösung des lin. Gls. muß 2n3/3 + O(n2) für
arithmetische Operationen und n2 + O(n) für Speicheroperationen als
Aufwand veranschlagt werden.
Verringerung der Rechenaufwandes
Es gibt unter anderem zwei Ansätze zur Verringerung des zum Teil
beträchtlichen Aufwandes.:
-
Wenn der Vektor x(k) noch weit von der gesuchten Lösung x* entfernt
ist, dann muß das lin. Gls. nur approximativ gelöst werden,
um einen trotzdem noch brauchbaren Vektor für den nächsten Iterationsschritt
zu erhalten. In der Praxis bedeutet das, daß die Lösung einer
Ungleichung genügen muß.
-
Es ist erfahrungsgemäß nicht immer notwendig nach jedem
Iterationsschritt den Vektor in die Jacobi- Matrix einzusetzen. Man kann
genauso gut mit den Werten des letzten Schrittes weiterrechnen. Das erspart
den n2 Teil des Aufwandes aus Punkt 3.
[ < ]
[ globale Übersicht ]
[ Kapitelübersicht ]
[ Stichwortsuche ]
[ > ]
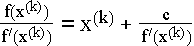
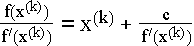
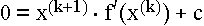
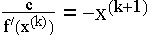
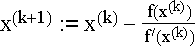
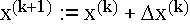
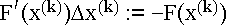
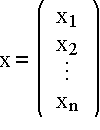
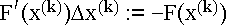 ,
das liefert ein lineares Gleichungssystem
,
das liefert ein lineares Gleichungssystem