Troger
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]

Newton-Verfahren

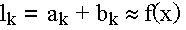
Wenn bei nichtlinearen Funktionen die Nullstellen x* nicht direkt bestimmt werden können, ersetzt man die Funktion durch eine lineare Funktion lk folgender Form:

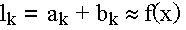
$l_k=\,a_k$ + b$_k\approx $ f$\left( x\right) $

Die Nullstellen xk* dieser Funktion werden als Näherung für die Nullstelle x* der ursprünglichen nichtlinearen Funktion verwendet.

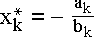
$x_k^{*}=-$ $\frac{a_k}{b_k}$

Wenn man ak und bk ausrechnet (mittels Abbruch der Taylor-Entwicklung um die Stelle x(k)), so erhält man folgende Form für die Nullstellen der Modellfunktion:

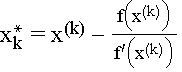
$x_k^{*}$ = x$^{(k)}-$ $\frac{f\left( x^{(k)}\right) }{f^\prime \left(x^{(k)}\right) }$

xk* ist nun eine bessere Näherung für x* als x(k), da man sich bei höherem k immer weiter der ursprünglich gewünschten Nullstelle nähert.

Es liegt also nahe, eine Folge { x(0), x(1), x(2),...} zu definieren, die die zuletzt berechnete Nullstelle als Startwert annimmt und eine neue Näherung berechnet, die dann noch näher bei x* liegt.

Die Folge

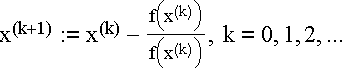
$x^{(k+1)}:=$ x$^{(k)}-$ $\frac{f\left( x^{(k)}\right) }{f\left( x^{(k)}\right)},$ $k=0,1,2,...$

konvergiert also gegen x* unter der Vorraussetzung, daß der Startwert x(0) nahe genug bei x* liegt.


Geometrische Bedeutung:

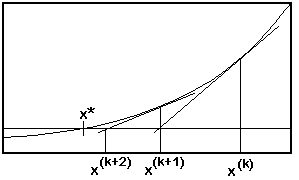
Im Punkt (x(0), f(x(0))) wird eine Tangente (erste Modellfunktion) an f gelegt und mit y=0 zum Schnitt gebracht. Dieser Schnittpunkt ist der neue Näherungswert x(k+1). An diesem Punkt wird dann die nächste Tangente angelegt und man erhält beim Schnitt wieder einen neuen Näherungspunkt x(k+1).


Konvergenz (Newton-Verfahren):

Für das Newton-Verfahren als iterativer Prozeß x(k+1) = t(x(k)) gilt

$t\left( x\right) $ =\thinspace x $-$ $\frac{f(x)}{f^\prime (x)}$ $und$$t^\prime (x)$ =\thinspace $\frac{f(x)f^{\prime \prime }(x)}{\left[ f^\prime(x)\right] ^2}$

Im Falle einer einfachen Nullstelle ist in einer Umgebung von x* die Ungleichung |t'(x)| < 1 wegen f(x*) = 0 sicher erfüllt, die Funktion t ist dort eine kontrahierende Abbildung. Durch Anwendung des Kontraktionssatzes sieht man, daß das Newton-Verfahren bei einem hinreichend guten Startpunkt x(0) stets gegen die einfache Nullstelle x* konvergiert. Ein guter Startpunkt heißt, daß der Startpunkt in der Nähe von x* liegen muß.


Konvergenzordnung (Newton-Verfahren):

Wenn man in der Formel für x(k+1) auf beiden Seiten die gesuchte Nullstelle abzieht erhält man

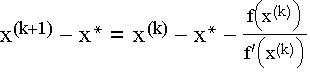
$x^{(k+1)}-$ x$^{*}=\,x^{(k)}-$ x$^{*}-\frac{f\left( x^{(k)}\right) }{f^\prime\left( x^{(k)}\right) }$

Falls x* eine einfache Nullstelle ist, d.h. wenn f(x*) = 0 und f'(x*) <> 0 gilt, dann folgt aus obiger Formel und der Entwicklung

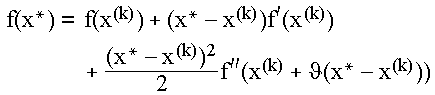
\EQN{7}{1}{}{}{\RD{\CELL{f(x^{\ast })=\,f(x^{(k)})+(x^{\ast }-x^{(k)})f^\prime(x^{(k)})}}{1}{}{}{}\RD{\CELL{ &&+\frac{(x^{\ast }-x^{(k)})^2}2f^{\prime \prime}(x^{(k)}+\vartheta (x^{\ast }-x^{(k)}))}}{1}{}{}{}}

mit

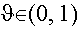
$\vartheta \varepsilon (0,1)$

die Beziehung

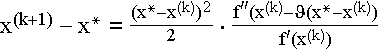
$x^{(k+1)}-x^{*}=\frac{(x^{*}-x^{(k)})^2}2\cdot \frac{f^{\prime \prime}(x^{(k)}-\vartheta (x^{*}-x^{(k)})}{f^\prime (x^{(k)})}$

und damit

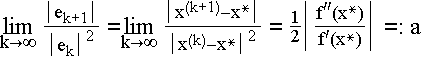
$\underset{k\rightarrow \infty }{\lim }\frac{\left| e_{k+1}\right| }{\left|e_k\right| ^2}=\underset{k\rightarrow \infty }{\lim }\frac{\left|x^{(k+1)}-x^{*}\right| }{\left| x^{(k)}-x^{*}\right| ^2}=\frac 12\left|\frac{f^{\prime \prime }(x^{*})}{f^\prime (x^{*})}\right| =:a$

Das Newton-Verfahren ist somit (bei einfachen Nullstellen und ausreichender Differenzierbarkeit von f) quadratisch konvergent und hat die Konvergenzordnung 1.


Mehrfache Nullstellen beim Newton-Verfahren:

Wenn x* eine mehrfache Nullstelle mit ganzzahliger Vielfachheit m={2,3,4,...} ist, so konvergiert wegen t'(x*) = 1(0). Die Konvergenzordnung ist jedoch nur 1, sodaß im Falle mehrfacher Nullstellen das Newton-Verfahren nur linear konvergiert.

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]