[ < ][ globale Übersicht ][ Kapitelübersicht ][ Stichwortsuche ][ > ]

8.5 Spezielle Matrixeigenschaften

Die Ausnutzung spezieller Matrixeigenschaften erweist sich bei der numerischen Lösung linearer Gleichungssysteme oft als nützlich. Es ist für den Anwender numerischer Software daher sehr wichtig, noch in der Planungsphase festzustellen, welche Strukturmerkmale seine Matrizen besitzen.

8.5.1 Symmetrische und Hermitesche Matrizen

Die transponierte Matrix A^T entsteht durch Spiegelung von A an der Hauptdiagonale:

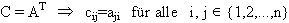
Der zu A^T gehörende lineare Operator wird als adjungiert bezeichnet. Für das innere Produkt gilt:

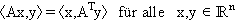
Eine symmetrische Matrix stimmt mit ihrer Transponierten überein, d.h.

so daß sie im inneren Produkt vom ersten auf den zweiten Vektor hinübergezogen werden darf:

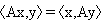
Diese Eigenschaft ist die formale Bedingung dafür, daß der zu A gehörende lineare Operator selbstadjungiert ist. Die selbstadjungierten Operatoren (und die zu ihnen gehörenden symmetrischen Matrizen) zeichnen sich durch spezielle Eigenschaften aus. So sind z.B. alle Eigenwerte eines selbstadjungierten Operators (einer symmetrischen Matrix) reell in die Eigenvektoren zu verschiedenen Eigenwerten sind orthogonal zueinander. Durch diese Eigenschaften nehmen die selbstadjungierten Operatoren in der Theorie und Praxis eine Sonderstellung ein.

Im Fall komplexer Matrizen 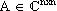spielt die Transposition A^T bzw. die Symmetrie keine so wichtige Rolle wie bei den reellen Matrizen. Von wesentlich größerer Bedeutung ist die konjugierte Transposition A^H:

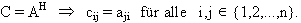
Matrizen mit der Eigenschaft A^H = A nennt man Hermitesche Matrizen.

8.5.2 Orthogonale und unitäre Matrizen

Orthogonale Matrix: Eine orthogonale Matrix ist eine quadratische Matrix Q 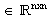mit orthogonalen Spaltenvektoren q₁,...,q_n. Sie erfüllt daher die Matrixgleichung:

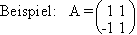
Unitäre Matrix: Eine komplexe Matrix 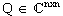mit der Eigenschaft

nennt man unitär.

8.5.3 Positiv definite Matrizen

Ein besonderer Typ von reellen symmetrischen bzw. komplexen Hermiteschen Matrizen mit einer speziellen Positivitätseigenschaft tritt in vielen Anwendungen auf. Reelle symmetrische Matrizen mit dieser Eigenschaft stellen eine Verallgemeinerung des Begriffs der positiven reellen Zahlen dar.

Zu jeder symmetrischen Matrix A gehört eine quadratische Form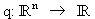

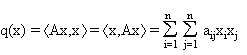
Falls 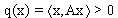für alle 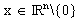gilt, heißt die quadratische Form q positiv definit.

Positiv definite Matrix: Eine Hermitesche n x n Matrix heißt positiv definit, wenn

Ist nicht die strenge Ungleichung erfüllt, sondern gilt nur x^HAx >=0, dann heißt A positiv semidefinit.

Regularität: Alle positiv definiten Matrizen sind regulär.

Indefinite Matrix: Fällt eine Hermitesche Matrix in keine der vorher genannten Klassen, nimmt also x^HAx für verschiedene Vektoren x negative und positive Werte an, so heißt A indefinit.

8.5.3.1 Kriterien für die Definitheit einer Matrix

• Die Diagonalelemente jeder positiv definiten Matrix sind positive reelle Zahlen.
• Jede Untermatrix einer positiv definiten Matrix ist positiv definit. Die Spur (also die Summe der Diagonalelemente), die Determinante und alle Minoren (das sind die Determinanten der Untermatrizen) einer positiv definiten Matrix sind positiv.
• Die Summe A + B zweier beliebiger positiv definiter Matrizen ist positiv definit.
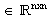• Sei A positiv definit. Ist C 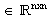, dann ist C^TAC positiv semidefinit. Ferner gilt rang(C^TAC) = rang(C), so daß C^TAC genau dann positiv definit ist, wenn rang(C) = m gilt.
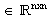• Eine symmetrische Matrix A ist positiv semidefinit genau dann und nur dann, wenn alle ihre Eigenwerte nichtnegativ sind. Sie ist positiv definit genau dann, wenn alle ihre Eigenwerte positiv sind. Ist A 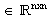positiv semidefinit, dann sind auch alle Potenzen A², A³,... positiv semidefinit.
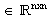• Ist A = (a_ij) symmetrisch und strikt diagonal dominant, also
  und gilt a_ii > 0 für alle i = 1, ... , n, dann ist A positiv definit.
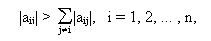
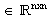• Sei A positiv semidefinit und k 1 eine natürliche Zahl. Dann existiert genau eine positiv semidefinite symmetrische Matrix B 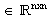, für die Folgendes gilt:
  
  1. B^k = A
  2. BA = AB und es existiert ein Polynom P(t), so daß B = P(A)
  3. rang(B) = rang(A); somit ist B genau dann positiv semidefinit, wenn A es ist.

8.5.3.2 Kongruenz von Matrizen

Zwei Matrizen A, B 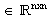heißen kongruent, wenn es eine reguläre Matrix C 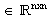gibt, so daß gilt:

[ < ][ globale Übersicht ][ Kapitelübersicht ][ Stichwortsuche ][ > ]