5.7.2 Implementierung arithmetischer Algorithmen

Autor: Martin Biribauer

Die Implementierung eines arithmetischen Algorithmus in Form eines Programms auf einem Computer mit Gleitpunktarithmetik ist normalerweise nicht äquivalent mit dem ihm zugrundeliegenden "exakten Algorithmus", der auf der Grundlage der reellen Zahlen und der zugehörigen arithmetischen Operationen entwickelt wurde, die man auf einem Computer nicht implementieren kann.

Selbst wenn die Daten Maschinenzahlen sind, ist ein implementierter arithmetischer Algorithmus im allgemeinen nicht äquivalent mit dem zugehörigen exakten Algorithmus. Der Grund liegt in der Nicht-Abgeschlossenheit von F bezüglich der exakten arithmetischen Operationen. Diese liefern nur in trivialen Sonderfällen für die Endresultate und alle Zwischenergebnisse wieder Zahlen aus der zugrundeliegenden Gleitpunkt-Zahlenmenge F.

Bei der Übertragung des in einer Programmiersprache formulierten Algorithmus in ein Objektprogramm müssen die arithmetischen Operationen durch die zu dem ausgewählten Maschinenzahlenbereich F gehörigen Pseudooperationen ersetzt werden (Kulisch, Miranker[271]). Der Objektcode realisiert also einen anderen Algorithmus als der Quellcode und damit auch eine andere mathematische Abbildung von den Daten in die Ergebnisse.

Es ist von fundamentaler Bedeutung für die Numerische Datenverarbeitttung, zu erfassen, wie sich die implementierte Abbildung von der "exakten" (d.h. der eigentlich im Bereich der reellen Zahlen beabsichtigten) Abbildung unterscheidet. Insbesondere ist es wichtig, zu erkennen, von welchen Eigenheiten eines Algorithmus, den man auch als Maschinenalgorithmus bezeichnet, erheblich oder nur geringfügig von denen des exakten Algorithmus unterscheiden.

Die Implementierungen äquivalenter arithmetischer Algorithmen liefern nämlich im allmgemeinen verschiedene Maschinenalgorithmen , die infolgedessen auch verschiedene Ergebnisse generieren,, weil sie ja unterschiedliche Zuordnungen zwischen Daten und Ergebnissen in F darstellen. Dabei kann es sein, daß sich die Ergebnisse von Implementierungen äquivalenter Algorithmen bezüglich ihrer Nähe zu den exakten Ergebnissen ganz wesentlich unterscheiden. Es ist dann ganz und gar nicht gleichgültig, welchen der äquivalenten Algorithmen man zur Lösung einer Aufgabe implementiert.

(S.219)

Beispiel (Quadratische Gleichung): Die Lösungen y₁ und y₂ der quadratischen Gleichung

sollen berechnet werden. Mit der Formel

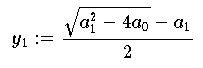
berechnet man zunächst y₁ und kann dann y₂ entweder als

oder als

bestimmen. Die beiden arithmetisch Algorithmen unterscheiden sich nur im letzten Schritt:

Wegen y₁+y₂=-a₁ und y₁*y₂=a₀ (nach dem, Wurzelsatz von Vieta) sind beide Algorithmen zur Berechnung von y₂ natürlich äquivalent.

Die Implementierung der Algorithmen QG-1 und QG-2 soll nun in der Gleitpunktarithmetik zum Zahlenbereich F(10,4,-9,9,true) mit optimaler Rundung (zur nächstgelegenen Maschinenzahl) untersucht werden. Ausgangspunkt sind die in F liegenden Daten a₁=-.5000*10¹ und a₀=-.1000*10⁰. Das exakte Ergebnis für diese Daten ist

Wie man leicht sieht, weichen die Zwischenergebnisse z₁, z₂ und z₃ im Maschinenalgorithmus nicht von den exakten Zwischenergebnissen ab, weil diese in F liegen. Erst bei

ergibt sich in der Implementierung

und ohne weiteren Rundungsfehler

Dann erhält man jedoch mit

Obwohl y₁=y₁ ist, also optimale Genauigkeit besitzt, erhält man ₂=y₂ nur mit dem Algorithmus QG-2, während sich bei QG-1 ₂ und y₂ beträchtlich (um ca. 0.4%) unterscheiden. Es wird sich herausstellen, dass kein Zufall ist.

(S.220)