4.2 Eigenschaften von Algorithmen

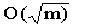
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]

4.2 Eigenschaften von Algorithmen

Im folgenden werden die bereits beim intuitiven Algorithmusbegriff und dem Beispiel Bisektion (4.1) aufgetretenen Eigenschaften genauer herausgearbeitet und diskutiert.

4.2.1 Abstraktion

Durch einen Algorithmus wird ein Problemlösungsprozeß auf einem bestimmten Abstraktionsniveau beschrieben, das durch die elementaren Algorithmen, die elementaren Objekte und den verwendeten Formalismus festgelegt wird.

Eine der wichtigsten Möglichkeiten der Abstraktion besteht darin, (Teil-) Algorithmen einen Namen zu geben und diesen Namen dann stellvertretend für die detaillierte Realisierung des Algorithmus zu verwenden.

Beispiel (BLAS) Die Programmpakete Blas-1, Blas-2 und Blas-3 sind heutzutage auf den meisten für die Numerische Datenverarbeitung eingesetzten Computern dauernd installiert. Den Programmentwicklern wird damit die Nutzung vorgefertigter Unterprogramme ermöglicht, mit denen sie elementare Probleme aus dem Bereich der Linearen Algebra lösen können. Die Unterprogramme können über ihre genormten Namen von anderen Programmen verwendet (aufgerufen) werden, was viel unnötige Programmarbeit (und vor allem Fehlersuche) erspart. Weiters kann bei der Verwendung der Blas-Programme davon ausgegangen werden, Software hoher Qualität, was Rechenzeit und Rechengenauigkeit betrifft, einzusetzen.

Die Blas-Programmpakete spielen schon bei der Erstellung neuer Programmkonzepte eine wichtige Rolle, indem sie Einheitlichkeit und Übersichtlichkeit fördern.

4.2.2 Allgemeinheit

Ein Algorithmus ist eine allgemeine Tätigkeitsbeschreibung, mit der nicht nur die Lösung einer einzelnen konkreten Aufgabe ermittelt wird, sondern die Lösung verschiedener (eventuell aller) Aufgaben einer bestimmten Klasse oder eines bestimmten Typs. Diese Problemklasse kann aus einer unendlichen Menge konkreter Aufgaben bestehen, die sich durch Daten (Parameter) voneinander unterscheiden. Die Auswahl eines einzelnen Problems erfolgt über dies Parameter.

Beispiel (Lineare Gleichungssysteme) Die Problemklasse der linearen Gleichungssysteme

Ax=b, mit A aus R^nXn, b,x aus Rⁿ
hat n²+n reelle Parameter:a₁₁,...,a_nn aus R und b₁,...,b_n aus R

Beispiel (Bisektion) Das Nullstellenproblem hat nicht nur die Zahlen a,b aus R, sondern auch eine auf [a,b] definierte Funktion f aus C[a,b] als Parameter. Bei diesem Problemtyp gibt es also sowohl algebraische als auch analytische Daten zur Spezifikation eines konkreten Problems.
Rechenbeispiel

4.2.3 Finitheit

Die Beschreibung eines Algorithmus besitzt nur eine endliche Länge (statische Finitheit). Ein Algorithmus kann auch, soll er je ein Resultat liefern (siehe Abschnitt 4.2.4), während seiner Ausführung nur endlich viel Platz zur Speicherung von Zwischenresultaten in Anspruch nehmen (dynamische Finitheit).

4.2.4 Terminierung

Einen Algorithmus nennt man terminierend, wenn er bei jeder Anwendung nach endlich vielen Verarbeitungsschritten anhält und ein Resultat liefert.

Das Terminieren einen Algorithmus darf nicht mit seiner Finitheit verwechslet werden. Es ist durchaus möglich, durch eine endliche Beschreibung einen Prozeß (z.B. mit Endlosschleife) zu definieren, der nicht nach endlicher Zeit beendet wird, also terminiert. Es gibt sogar Algorithmen mit praktischem Nutzen, die (potentiell) "endlos laufen", z.B. Algorithmen zur Steuerung "nichtabbrechender" Vorgänge (z.B. in chemischen Produktionsstätten) oder das zentrale Steuerungsprogramm (Betriebssystem) einen Computers, der Tag und Nacht in Verwendung steht.

Die Überlegungen und Beispiele dieses Buches beschäftigen sich ausschließlich mit terminierenden Algorithmen.

Beispiel (Bisektion) Beim Bisektionsverfahren kann das Terminieren auf verschiedene Arten erreicht werden. Dabei ist grundsätzlich zu unterscheiden, ob eine als Ergebnis des Verfahrens akzeptable Näherungslösung x^~ entweder durch die Eigenschaft f(x^~) ~ 0 (Residuums-Kriterium) oder durch ihre Nähe x^~~x^* zu einer Nullstelle mit f(x^*)=0 (Fehler-Kriterium) charakterisiert werden soll. Im einen Fall wird man den Prozeß beenden, wenn |f(x^~)| <= T_f erreicht wird, im anderen Fall, wenn die Länge des zuletzt erhaltenen Intervalls eine Bedingung der Art (b-a)/2^k < T_k erfüllt.
Rechenbeispiel

Man beachte, daß man im ersten Fall a priori, also vor Ausführung des Verfahrens, nicht sagen kann, wann (also nach wievielen Intervallhalbierungen) es terminieren wird (wenn man von Schwierigkeiten absieht, die von der Maschinenarithmetik herrühren können). Beim zweiten Abbruchkriterium kann amn hingegen von vornherein sagen, nach wievielen Intervallhalbierungen der Prozeß spätestens terminieren wird.

Bei manchen Daten kann sich ein Algorithmus als unanwendbar erweisen; in diesem Fall sollte der Lösungsprozeß mit einer entsprechenden Mitteilung abgebrochen werden.

Beispiel (Bisektion) Der Bisektionsalgorithmus ist nur anwendbar, wenn die Funktion, deren Nullstelle bestimmt werden soll, an den Endpunkten des Ausgangsintervalls Werte mit verschiedenen Vorzeichen besitzt. Diese Voraussetzung ist leicht zu überprüfen.

Eine andere wichtige Voraussetzung des Bisektionsverfahrens ist die Stetigkeit von f. Wenn diese Voraussetzung nicht erfüllt ist, kann es unter Imständen dazu kommen, daß der Algorithmus nicht terminiert. Wenn z.B. die Bisektion auf dem Intervall [0,1] für

f(x)= -1 für x <=0.1 und f(x)= +1 für x>0.1

ausgeführt wird, so terminiert sie nicht.

Dieses Beispiel beleutet eine fundamentale Schwierigkeit numerischer Algorithmen: Aus einer endlichen Menge von Werten - bei der Bisektion sind dies die Funktionswerte f(a), f(b), f((a+b)/2),... - kann nicht auf ein Kontinuum, z.B. auf die Eigenschaft der Stetigkeit von f, geschlossen werden. Eine algorithmisch formulierte (in einem Programm automatisch ablaufende) Überprüfung der Stetigkeitsvoraussetzung ist daher prinzipiell unmöglich.

Es liegt im Verantwortungsbereich des Anwenders, zu überprüfen, ob alle Voraussetzungen erfüllt sind, oder sich zumindest der möglichen Konsequenzen einer Nicht-Erfülltheit voll bewußt zu sein.

Die Voraussetzung für die Anwendbarkeit eines Algorithmus klar zu formulieren, ist ein notwendiger Teil der Dokumentation von Algorithmen.

4.2.5 Determinismus

Einen Algorithmus nennt man deterministisch, wenn zu jedem Zeitpunkt seiner Ausführung höchstens eine Möglichkeit der Fortsetzung besteht, also der Folgeschritt eindeutig bestimmt ist. Besteht keine Möglichkeit zur Fortsetzung der Ausführung, so vereinbart man, daß der Algorithmus terminiert.

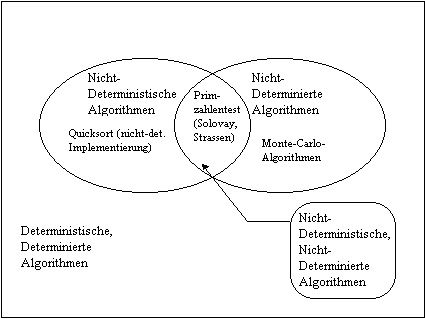
Hat ein Algorithmus an mindestens einer Stelle zwei oder mehr möglichkeiten der Fortsetzung, von denen eine nach belieben ausgewählt werden kann, so heißt er nichtdeterministisch.

Nichtdeterministische Algorithmen, bei denen man den alternativen Fortsetzungsmöglichkeiten Wahrscheinlichkeiten zuordnen kann, nennt man stochastische Algorithmen. Derartige Algorithmen entwickelt man häufig für Probleme, zu deren Lösung ein deterministischer Algorithmus zu viel Zeit benötigt.

Beispiel (Primzahlentest) Von R. Solovay und V. Strassen stammt ein stochastischer Algorithmus zur Entscheidung, ob eine vorgegebene Zahl m eine Primzahl ist oder nicht. Falls der Algorithmus das Resultat "nein" liefert, so ist gesichert, daß m keine Primzahl ist. Liefert der Algorithmus hingegen das Resultat "ja", so weiß man nur, daß diese Antwort mit einer Wahrscheinlichkeit p>=0.5 korrekt ist. Die Sicherheit der Entscheidung kann man verbessern, indem man den Algorithmus mit demselben Eingangswert öfter aufruft. Bei k-maligem Aufruf verringert sich dann die Wahrscheilichkeit p_k einer Fehlentscheidung auf 2^-k. Jede noch so kleine Irrtumswahrscheinlichkeit ist unterschreitbar:

p_k	1%	0.1%	0.01%	0.001%
k>=	7	10	14	17

Die beim Solovay-Strassen-Algorithmus nicht vermeidbare Unsicherheit bei der Entscheidung "m ist eine Primzahl" wird, speziell bei sehr großen Zahlen (die z.B. bei Verschlüsselungsverfahren auftreten), durch einen deutlich verringerten Rechenaufwand aufgewogen. Während ein naheliegender deterministischer Algorithmus

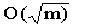
$O(\sqrt m)$
Rechenoperationen benötigt (um für
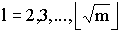
$l=2,3,...,\lfloor \sqrt m \rfloor$
zu probieren, ob m geteilt wird), verringert der stochastische Algorithmus den Aufwand auf O(k.log m) Rechenschritte (vgl. Abschnitt 4.5).

4.2.6 Determiniertheit

Ein Algorithmus heißt determiniert, wenn er mit den gleichen Parametern und Startbedingungen stets das gleiche Ergebnis liefert.

Einen numerischen Algorithmus A kann man als eine Abbildung A:E->A von der Menge E der möglichen Eingabewerte in die Menge A der möglichen Ausgabewerte auffassen. Bei einem determinierten Algorithmus ist diese Abbildung eine Funktion im mathematischen Sinn, jedem Eingabewert entspricht also genau ein Ausgabewert.

Determinismus und Determiniertheit sind auseinanderzuhalten:Determinismus kennzeichnet einen Algorithmus, bei dem der gesamte Ablauf eindeutig bestimmt ist. Determiniertheit bezieht sich nur auf die eindeutige Bestimmtheit des Resultats. Deterministische Algorithmen haben durch ihren eindeutigen Ablauf auch ein eindeutiges Resultat, sie sind daher stets determiniert. Die Umkehrung gilt jedoch nicht: es gibt nichtdeterministische Algorithmen, die über verschiedene Wege stets zum gleichen Ziel kommen, also determiniert sind.

Beispiel (Quicksort) Das Quicksort-Verfahren ist ein schnelles Sortierverfahren, das auf dem rekursiven Sortieren von Teilfeldern beruht. Die Unterteilung in Teilfelder kann stochastisch erfolgen, sodaß der Ablauf nicht eindeutig bestimmt ist. Das Resultat ist aber stets dasselbe: das sortierte Feld. Das stochastische Quicksort-Verfahren ist also trotz des nichtdeterministischen Ablaufs ein determinierter Algorithmus.

Beispiel (Primzahlentest) Der stochastische Primzahlentest von R. Solovay und V. Strassen ist sowohl nichtdeterministisch, d.h. der Ablauf ist nicht eindeutig bestimmt, als auch nichtdeterminiert, d.h., das Resultat kann anders ausfallen, wenn man den Vorgang wiederholt.

Monte-Carlo-Algorithmen

Unter dem Begriff der Monte-Carlo-Methode faßt man eine Vielzahl von Verfahren zur numerischen Lösung verschiedener mathematischer Probleme zusammen, die alle auf Erkenntnissen und Techniken der Wahrscheinlichkeitstheorie und der mathematischen Statistik beruhen.

Die Monte-Carlo-Methode ist durch folgende Schritte charakterisiert:

Für das vorliegende (determinierte) Problem wird ein stochastisches Modell entwickelt.
Mit diesem Modell werden - mit Hilfe von (Pseudo-) Zufallszahlen - am Computer Experimente (Simulationen) ausgeführt.
Die Ergebnisse der Zufallsexperimente wertet man mit Methoden der statistischen Schätztheorie aus.
Die erhaltenen statistischen Schätzwerte werden als (Näherungs-) Lösung des ursprünglichen mathematischen Problems interpretiert.

Die Monte-Carlo-Methode kan z.B. zur Berechnung von Integralen (siehe Rechenbeispiel) ,zurLösung partieller Differentialgleichungen oder zur Lösung algebraischer Gleichungssysteme eingesetzt werden. Besonders vorteilhaft ist ihr Einsatz, wenn es sich um mehrdimensionale Probleme handelt (Kalos,Whitlock [59]).

Monte-Carlo-Algorithmen, die man durch Anwendung der Monte-Carlo-Methode auf spezielle Problemklassen (z.B. numerische Integrationsprobleme, siehe Abschnitt 12.4.4) erhält, sind nichtdeterminiert. Bei jeder Wiederholung eines Monte-Carlo-Algorithmus mit anderen Zufallszahlen erhält man auch andere Ausgabewerte.

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]