Wir simulieren
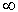durch einen wachsenden Wert von n, den wir bis
über die maximale Maschinenzahl steigern, also über 8.98847E+307.
Man sollte annehmen, daß wir uns mit den wachsenden Wert von n, der Zahl e 2.718281828459045235360287471352662497757...
kontinuierlich nähern.
In der Tat, ist dies aber nicht der Fall:
| n | angenäherter Wert | n | angenäherter Wert |
|---|---|---|---|
| 1 | 2 | 1.8010E+15 | 3.319144272339289 |
| 2 | 2.25 | 1.8015E+15 | 2.225600376922854 |
| 3 | 2.37037037037037 | ... | ... |
| .. | ... | 3.00E+15 | 3.789627121971632 |
| 1E+03 | 2.716923932235594 | 3.01E+15 | 1.995102380751929 |
| 1E+04 | 2.718145926824925 | ... | ... |
| 1E+05 | 2.718268237192297 | 8E+15 | 5.908292303942209 |
| ... | ... | 9E+15 | 7.377253717268280 |
| 1E+11 | 2.718282053357110 | 9.01E+15 | 1 |
| 1E+12 | 2.718523496037238 | ... | ... |
| 1E+13 | 2.716110034086901 | 1E+307 | 1 |
| ... | ... | 8.988465E+307 | 1 |
| 9.25E+13 | 2.735781599480060 | 8.988466E+307 | 2.718281828459045 |
| 9.50E+13 | 2.695083429407301 | 1E+308 | 2.718281828459 |
Der Rechner zeigt Resultate die sich gegen unserer Erwartung verhalten.
Lassen wir n kontinuierlich steigen, so scheint sich der errechnete Wert e zu nähern, überschreitet diesen und fällt dann auf einen Wert der unter e liegt zurück. Dies wiederholt sich mit immer größeren Ausschlag, so daß schließlich ein Extemwert von 7.377253717268280 erreicht wird. Steigert man n auf 9.01E+15 fällt der Wert auf 1, und bleibt auf 1, bis zur Erreichung der maximalen Maschinenzahl, also bis 8.988465E+307. Bei n = 8.988466E+307 und darüber, springt das Resultat auf den richtigen Wert von e, was offensichtlich damit zusammen hängt, daß Mathematica mit n
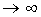rechnen kann.
Der Verlauf der Näherungsrechnung läßt sich am besten durch nachstehendes Diagramm demonstrieren.
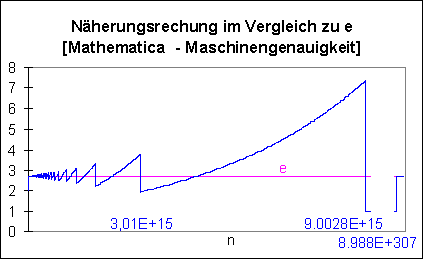
Wir werden im folgenden sehen, daß die Charakteristik dieser Annäherung gleich der Ergebnisse der Näherungsrechnung mit Turbo C mit doppelter Genauigkeit (double precision) ist.
Das unstetige Verhalten der Näherungskurve hängt mit der Rundungsarithmetik zusammen und wird bei der Berechnung mit Turbo C erörtert. Auch die Darstellung des absoluten und relativen Fehlers findet sich bei Turbo C.
