Bisektionsverfahren

Eine Besonderheit des skalaren Falles ist die Möglichkeit, aus unterschiedlichen Vorzeichen der Funktionswerte an den Enden eines Intervalls auf die Existenz einer Nullstelle im Intervall zu schließen.

Satz:

Ist die Funktion

stetig, gilt also f ist aus C[a,b], so nimmt f auf [a,b] jeden Wert zwischen f (a) und f (b) mindestens einmal an.

Wenn die Werte f (a) und f (b) einer auf [a,b] stetigen Funktion verschiedenes Vorzeichen besitzen, so gibt es also mindestens einen Punkt

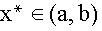
mit f (x^*) = 0. Die existenz einer Nullstelle ist damit gesichert.

Beim Bisektions- Algorithmus werden Intervall- Halbierungen solange durchgeführt, bis das Intervall, von dem man sicher weiß, daß es eine Nullstelle von f enthält, so klein wie gewünscht ist.

Start- Intervall :[x_links,x_rechts] mit f(x_links) f(x_rechts) < 0

do k=1,2,3,.....
   xmitte:=(xlinks+xrechts)/2;
   if f(xlinks)*f(xmitte) < 0 then xrechts:=xmitte
                            else xlinks:=xmitte
   if Abruchkriterium erfüllt then exit
end do

Beim Bisektions- Algorithmus (continous binary search) wird eine adaptive Diskretisierung zur Informationsgewinnung verwendet: Die Entscheidung, wo die nächste Auswertung der Funktion f vorzunehmen ist, kann nur auf Grund der gesamten bereits verfügbaren Information getroffen werden.

Bemerkung: Optimalität der Bisektion

Für stetige Funktionen mit Vorzeichenwechsel ist die Informationsgewinnung durch Bisektion optimal: Der Bisektionsalgorithmus liefert - im Sinne einer Worst-Case Analyse - von allen Nullstellenalgorithmen eine Nullstelle mit geforderter Genauigkeit mit der geringsten Anzahl von f-Auswertungen.

Hat man zwei Stellen a,b mit unterschiedlichen Vorzeichen von f gefunden, dann ist die Konvergenz des Bisektions- Algorithmus garantiert. Bei den Nullstellenverfahren der nächsten Abschnitte (Newton-Verfahren, Sekanten-Verfahren) gibt es im allgemeinen kein praktikables Kriterium, das sicherstellt, daß x(0) im Einzugsbereich der Lösung liegt.

Das Bisektionsverfahren setzt nur die Stetigkeit der Funktion f - nicht deren Differenzierbarkeit - voraus. Es konvergiert dafür linear mit dem Konvergenzfaktor 1 / 2. Nach k Funktionsauswertungen im inneren des Startintervalls hat sich die aktuelle Intervall- Länge l = x_rechts-x_links auf das 2-k-fache der Länge lstart des Startintervalls reduziert. Folgende absolute Genauigkeiten werden daher sicher erreicht:

       k                10      20      40       80

       Epsilon abs      10-3   10-6     10-12    10-24

Um eine Verdopplung der Anzahl der gültigen Stellen zu erreichen bzw. Garantieren zu können, muß die Schrittanzahl des Bisektions- Verfahrens verdoppelt werden. Bei einem quadratisch konvergenten Verfahren ( wie z.B.: dem Newton Verfahren) genügt hierfür ein einziger zusätzlicher Schritt.

l_start / 2k ist eine obere Schranke für den absoluten Fehler von x(k) , die unter Umständen stark unterschritten wird.

Beispiel:

Für f(x) := xe^-x - 0.06064 gilt

f(0) = - 0.06064 < 0 und f(1) = 0.30723944..... > 0.

Da f eine stetige Funktion ist, liegt im Intervall [0,1] sicher mindestens eine Nullstelle, die mit dem Bisektions- Algorithmus bestimmt werden kann. Nach k=12 Halbierungsschritten wird mit x_mitte=6.469727*10^-2 ein Wert erreicht , der einen absoluten Fehler von 4.63 * 10^-6 aufweist. Die Fehlerschranke würde eine solche Genauigkeit erst bei k=18 garantieren. Bemerkenswert ist jedoch, daß beim nächsten Halbierungsschritt ( k=13 ) der absolute Fehler von x_mitte 6.457520*10^-2 den wesentlich größeren Wert -1.17*10^-4 aufweist, der deutlich näher bei der Fehlerschranke 2-13 =1.22*10^-4 liegt.

Dieses Beispiel zeigt, daß das Fehlerverhalten der Bisektions- Interation mit wachsendem k im allgemeinen nicht monoton ist.

Das Bisektionsverfahren läßt sich im Gegensatz zu Newton- und Sekanten- Verfahren nicht auf n > 2, d.h. auf nichtlineare Gleichungssysteme, übertragen.