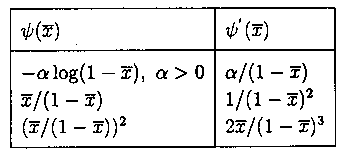[ < ]
[ globale Übersicht ]
[ Kapitelübersicht ]
[ Stichwortsuche ]
[ > ]
7.2.3 Transformation des Integrationsbereiches
Bevor man mit der numerischen Integration beginnen kann muß darauf geachtet werden, daß der Integrationsbereich überhaupt numerisch verarbeitbar ist. So müssen zum Beispiel uneigentliche auf eigentliche Bereiche abgebildet werden oder allgemeine Bereiche auf Standartbereiche, da sich die Anwendungsgebiete der Integrationsalgorithmen meist nur auf diese Bereiche beschränken.
Eine sehr wichtige Rolle bei den Transformationen des Integrationsbereiches spielt die Jacobi-Matrix J. Mit ihrer Hilfe kann bei mehrdimensionalen Funktionen ein Standardbereich auf den Integrationsbereich abgebildet werden (Zu beachten ist die Richtung der Abbildung, die bei der Herleitung der Transformationsregeln umgekehrt wird).
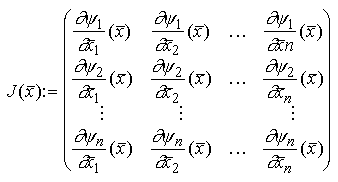
Durch die Jacobi-Matrix können Transformationsregeln abgeleitet werden. Die vereinfachte mehrdimesionale Transformationsregel lautet:
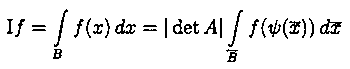
Ein wichtiger Spezialfall sind dabei univariate Funktionen, bei denen man vereinfachte Transformationsregeln anwenden kann, je nachdem ob die Determinante von J größer oder kleiner Null ist.
![\begin{array}{lcll}
\displaystyle \int \limits_{B}{f(x )\,dx } & = &
\displaystyle \int \limits_{\overline{B}} {f(\psi(\overline{x } )) \cdot
\psi'(\overline{x } ) \,d\overline{x } }
~~~~~~~&\mbox{fur}\quad\psi'>0,\\[3ex]
\displaystyle \int \limits_{B}{f(x )\,dx } & = &
\displaystyle - \int \limits_{\overline{B}} {f(\psi(\overline{x } )) \cdot
\psi'(\overline{x } ) \,d\overline{x } }& \mbox{fur}\quad\psi'<0.
\end{array}](pic/g02_0303.gif)
Ziel ist es, den Integrationsbereich auf einen standardisierten Bereich abzubilden und somit die Anwendung von Integrationsformeln, die sich auf diese Bereiche beschränken, zu ermöglichen.
Mit Hilfe von Transformationstabellen können unbeschränkte Bereiche auf beschränkte übergeführt werden. So können zum Beispiel die Bereiche [0, unendlich) in [0, 1).
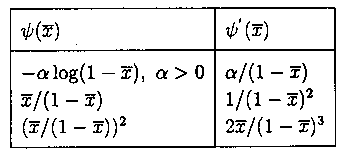
oder (-unendlich, unendlich) in [-1, 1] umgewandelt werden.

Da Integrale additiv bezüglich der Zerlegung des Integrationsbereiches sind, bietet sich die Anwendung verschiedener Algorithmen bei sehr komplexen Problemen an. Jedes Teilstück des Integrationsbereiches wird von dem Algorithmus behandelt, der am besten geeignet ist.
Die Iteration von Integralen bedeutet das Zurückführen von mehrdimensionalen Integrationsproblemen auf Integrale mit einer geringeren Dimension, um diese Integrale leichter berechnen zu können.
Zu beachten ist, daß die Reihenfolge der Iterationen einen entscheidenden Einfluß auf den Aufwand der numerischen Berechnungen hat.
[ < ]
[ globale Übersicht ]
[ Kapitelübersicht ]
[ Stichwortsuche ]
[ > ]
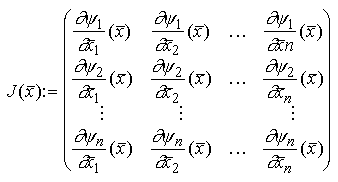
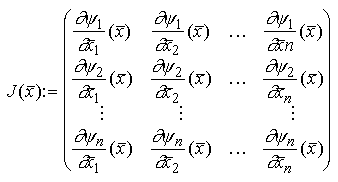
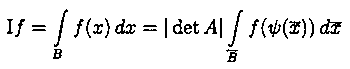
![\begin{array}{lcll}
\displaystyle \int \limits_{B}{f(x )\,dx } & = &
\displaystyle \int \limits_{\overline{B}} {f(\psi(\overline{x } )) \cdot
\psi'(\overline{x } ) \,d\overline{x } }
~~~~~~~&\mbox{fur}\quad\psi'>0,\\[3ex]
\displaystyle \int \limits_{B}{f(x )\,dx } & = &
\displaystyle - \int \limits_{\overline{B}} {f(\psi(\overline{x } )) \cdot
\psi'(\overline{x } ) \,d\overline{x } }& \mbox{fur}\quad\psi'<0.
\end{array}](pic/g02_0303.gif)