5.7.4 Analyse der Fehlerfortpflanzung

Wenn in einem Algorithmus nur ein einziger Rechenfehler entsteht (wie es im Beispiel der Quadratischen Gleichung bei Algorithmus QG-1 der Fall war), dann kann man die Empfindlichkeit der Endergebnisses bezüglich dieser Störung folgendermaßen erfassen:

Angenommen, der Fehler entsteht bei der Berechnung des Zwischenergebnisses z_i, sodaß man anstelle des exakten Wertes z_i das Resultat _i erhält. Dann betrachtet man den verbleibenden Teil des arithmetisch Algorithmus nach der Berechnung von zi als einen eigenen Algorithmus: den "Restalgorithmus nach z_i". Dieser hat als Daten jene des ursprünglichen Algorithmus - a₁,a₂,...a_m - und die bisher errechneten Zwischenergebnisse z₁,z₂...z_i, soweit sie im RestAlgorithmus noch explizit vorkommen. Der Wert zi selbst gehört in jedem Fall zu den Daten des Restalgorithmus, sonst wäre seine Berechnung sinnlos gewesen. Die Endresultate des Restalgorithmus sind dieselben wie die des ursprünglichen Algorithmus.

Kondition bezüglich der Zwischenergebnisse

Für den Restalgorithmus kann man wie für jeden anderen Algorithmus die Kondition bezüglich der änderung seiner Daten, insbesondere bezüglich der änderugnen von z_i, definieren, indem man die Empfindlichkeit seiner Ergebnisse bezüglich dieser änderungen betrachtet. Diese Empfindlichkeit kann man wieder mit Hilfe von Konditionszahlen (siehe Kapitel 2) quantitativ erfassen, Damit kann man dann die änderung des Endresultates des ursprünglichen Algorithmus auf Grund der Abänderung von z_i in _i abschätzen.

(S.222)

Beispiel (Quadratische Gleichung) Der Restalgorithmus nach z₄ lautet:

Daten sind a₁ und z₄ in der Version QG-1 bzw. a₁,a₀ und z₄ in der Variante QG-2.

Die durch QG-1 vermittelte mathematische Abbildung (a₁,z₄)->y₂ lautet

und die relative Konditionszahl (Grenzkondition, siehe Kapitel 2)

ist für den Einfluss einer Änderung von z₄ auf die relative Genauigkeit von y₂ maßgeblich. Für a₁=-5 und z₄~5.04 ergibt sich

was die festgestellt Vergrösserung des relativen Fehlers um mehr als 2 Grössenordnungen erklärt.

Auf diese Weise kann man im Prinzip⁷ bei jedem arithmetischen Algorithmus seine Kondition bezüglich einer Änderung jedes einzelnen Zwischenergebnisses untersuchen. Allerdings beziehen sich die so gewonnenen Konditionszahlen auf die artifizielle Situation, dass sich nur das jeweils betrachtete Zwischenergebnis ein wenig ändert und der Algorithmus sonst exakt abläuft. Eine derartige Situation liegt natürlich in der Praxis nie vor. Es ist jedoch fast immer der Fall, dass die direkten Auswirkungen eines gestörten Zwischenergebnisses auf das Eindergebnis wesentlich stärker sind als die indirekten Effekte überr eine geringfügige änderung des Restalgorithmus selbst, etwa durch eine Beeinflussung der Details der Rundungsvorgänge.

In einer Analyse der Fehlerfortpflanzungseigenschaften geht es in erster Linie darum, qualitativ festzustellen (etwa grössenordnungsmässig), ob die Konditionszahlen bezeuglich der Zwischenergebnisse diejenigen des GesamtAlgorithmus bezüglich seiner Daten deutlich übertreffen oder nicht. Man ist ja in der Praxis nicht einmal in der Lage (wegen des damit verbundenen prohibitiven Aufwands), die Konditionszahlen auch nur annäherungsweise zu berechnen.

Umso wichtiger ist es, zu erkennen, welche Situation in einem arithmetisch Algorithmus regelmässig zu einer Verschlechterung seiner Stabilität führen. Es wird sich heraussetllen, das hiefür fast immer eine typische artih. Konstellation verantwortlich ist, di sich bei insgesamt gut konditionierten Abbildungen zwischen Daten und Ergebnis durch geeignete Gestaltung eines arithmetischen Algorithmus oft vermeiden lässt. Zu diesem Zweck wird im nächsten Abschnitt die Kondition dereinzelnen arithmetisch Operationen untersucht.

⁷ Daß eine solche Analyse stetige Differenzierbarkeit der untersuchten Zusammenhänge voraussetzt, ist noch das geringere Problem, weil sich die detaillierte Untersuchung eines komplizierten Algorithmus wegen des damit verbundenen Aufwands von selbst verbietet.

(S.223)

Fehlerfortpflanzung in Einzeloperationen - Auslöschung

Im folgenden wird die Empfindlichkeit einzelner exakter arithmetischr Operationen auf änderungen in ihren "Daten", d.h. in ihren Operanden untersucht. Da es in einer Gleitpunktarithmetisch fast immer um eine relative Größe von Änderungen, Störungen und Fehlern geht - "wieviele Stellen der Mantisse sind richtig ?" - beschränkt man sich bei der Analyse von Auswirkungen der Fehlerfortpflanzung meist auf die Untersuchung der reltiaven Kondition und die Ermittlung relativer Konditionszahlen (siehe Kapitel 2). Die absolute Kondition einzelner Operationen spielt für die Fehlerfortpflanzung nur äusserst selten eine maßgebliche Rolle.

Schlechte relative Kondition bedeutet für eine Einzeloperation, dass sich die Änderung eines Operanden an einer hinteren (weniger wichtigen) Stellen der Mantisse seinerr Gleitpunktdarstellung auf vorderen (bedeutsamen) Stellen der Mantisse des Ergebnisses auswirkt. Diese unerwünschte Situation ergibt sich am häufigsten durch Auslöschung führender Stellen (cancellation of leading digits) bei Addtition / Subtraktion zweier annähernd (gegen-)gleicher Zahlen mit vberschieden/gleichen Vorzeichen. In diesem Fall heben einander die vorderen, übereinstimmenden Mantissenstellen der beiden Operanden auf; Störungen an einer hinteren Mantissenstelle der Daten werden im Ergebnis zu einer Störung an einer vorderen Stelle.

Beispiel (Auslöschung) Es soll die Differenz der annähernd gleichgrossen Zahlen a und b berechnet werden:

Verändert man a um 0.00007 , das ist eine relative Änderung von 10^-5 , in ã=7.64359 , dann ändert sich die Differenz natürlich auch nur um 0.00007 in a-b=0.00073. Die relative Änderung der Differenz ist hingegen erheblich grösser, nämlich

Im Gleitpunktzahlensystem F(10,6,-9,9,true) ergibt sich

Eine änderung der letzten Stelle der Mantisse von a hat eine Änderung an der ersten Stelle der Mantisse der Differenz a-b bewirkt !

Besonders zu beachten ist die Tatsache, dass im Fall der Auslöschung kein Rechenfehler auftritt. Der grosse relative Fehler des Resultats ist auschliesslich auf die bereits vor der ausgeführten arithmetischen Operation vorhandenen Fehler der Operanden (Daten) zurückzuführen.

Auslöschungssituationen sind die mit Abstand häufigste Ursache für Instabilität arithmetischer Algorithmen. Die lokale Verstärkung des relativen Effekts der Änderung (Störung) einer Eingangsgrösse kann im allgemeinen auch nicht mehr rückgängig gemacht werden.

Kondition von Addition und Subtraktion

Autor: Berndt Schiebeck

Aus den beiden Formeln

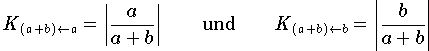
für die Konditionszahlen der Addition und den analogen Formeln für die Konditionszahlen der Subtraktion (alle + durch - ersetzen) erhält man folgende Formeln für die Summe von Operanden mit verschiedenen Vorzeichen:

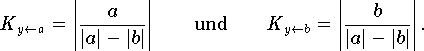
Die Beträge werden nur verwendet, um nicht für Addition und Subtraktion zweimal dieselbe Formel anzuschreiben.

Wenn das Ergebnis von a - b betragsmäßig sehr viel kleiner ist als die beiden Operanden a und b, werden die Konditionszahlen sehr viel größer als 1. Ist b sehr viel kleiner als a, so ist die Konditionszahl von b ebensoviel kleiner als 1, und eine Änderung von b wirkt sich auf das Resultat a - b relativ gering aus.

Bei der Addition von Operanden mit gleichem Vorzeichen ergibt sich

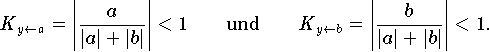
Ist b sehr viel kleiner als a, so ist die Konditionszahl von b ebensoviel kleiner als 1, und eine Änderung von b wirkt sich auf das Resultat a + b relativ wenig aus.

Kondition von Multiplikation und Division

Eine Multiplikation y = a • b ist wegen

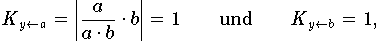
von der Größenordnung und der Vorzeichen der beiden Operanden unabhänging und somit eine gänzlich harmlose, gut konditionierte Operation.

Bei der Division y = a / b gilt

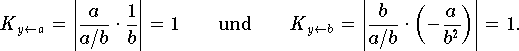
Daher gibt es - im Gegensatz zur Addition und Subtraktion - keine Fehlerverstärkung.

Kondition von Standardfunktionen

Auch bei den Standardfunktionen tritt nur in gewissen Fällen eine Fehlerverstärkung auf, wiederum wenn ein kleiner Funktionswert für ein Argument entsteht, das nicht in der Nähe von Null liegt z.B.:

• Bei logarithmischen Funktionen y = log(a) = c•ln(a) mit a ~ 1
  

• Bei trigonometrischen Funktionen, z.B. bei y = sin(a) in einer engen Umgebung einer von Null verschiedenen Nullstelle (für a)
  

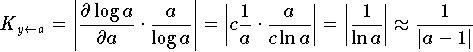
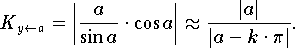
  Hingegen ist für a in einer engen Umgebung von Null diese Operation eine für die Fehlerfortpflanzung harmlose:

  

Hintergrund der Konditionszahlberechnungen und deren Verwendungszweck

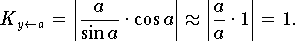
Welchen tieferen Sinn hat nun die Berechnung der Konditionszahlen für den Entwurf von Algorithmen ?

Bei dem Entwurf eines numerischen Algorithmus, muß man stets darauf achten, daß keine Auslöschungssituation auftritt. Die Auslöschung ist die einzige Grundsituation, die zur Instabilität numerischer Algorithmen führt.
Das Vermeiden von Auslöschung ist aber nicht einfach, da der Effekt ja von den Werten der beteiligten Variablen abhängt. Die Addition von annähernd gleich großen Zahlen mit verschiedenem Vorzeichen ist "gefährlich". Um Instabilitäten in Programmen zu vermeiden, müßte ein Test auf ein Vorliegen einer solchen Situation durchgeführt werden, und eine vom Ausgang des Tests abhängige Verzweigung vorgenommen werden.

Beispiel: Berechnung eines trigonometrischen Ausdrucks

Die Berechnung des Wertes

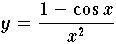
ist für x-Werte in der Nähe von 0 eine gut konditionierte Aufgabe. Die Taylorentwicklung von cos x zeigt, daß für kleine |x|

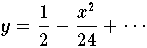
gilt, ein kleine relative Änderung von x läßt den Wert von y praktisch unverändert.

Bei der numerischen Berechnung nach

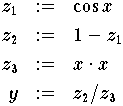
erhält man aber wegen 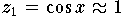starke Auslöschung bei der Berechnung von z₂. Der Rundungsfehler, der bei der Gleitpunktberechnung von z₁ ensteht, verfälscht in stark vergrößerndem Ausmaß das Endergebnis.

Berechnet man aber obigen Ausdruck mit Hilfe der trigonometrischen Identität

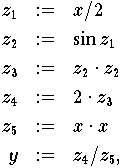
dann hängt das Endergebnis nur in harmloser Weise vom Zwischenergebnis z2 ab.

Autor: Markus Flatscher

GESAMTANALYSE EINES ARITHMETISCHEN ALGORITHMUS

Bei der Implementierung eines realistischen (d.h. eines aus sehr vielen Einzeloperationen bestehenden) arithmetischen Algorithmus in einer Gleitpunktarithmetik ergibt sich im allgemeinen in jedem Schritt folgende Situation:

1. Die Operanden der durchzuführenden Operation sind Zwischenergebnisse vor- angegangener Berechnungnen, die bereits durch Rundungsfehler verfälscht sind.

2. Das Ergebnis der Operation liegt nicht in FF, es muss also gerundet werden, wodurch ein weiterer Fehler neu entsteht.

Während im Kapitel 3 die Entstehung von Rundungsfehlern behandelt wurde, waren die bisherigen Teile von Abschnitt 5.7 vornehmlich der Auswirkung einzelner Operationsfehler aufdas Ergebnis gewidmet. Eine detaillierte Analyse der überlagerung all dieser Einzeleffekte in einem grössereren Algorithmus ist in der Praxis völlig unmöglich. Sie ist aber auch meist nicht nötig: Ist nämlich jeder einzelne Rundungsfehler "sehr klein", wie es bei der Verwendung eines Gleitpunkt-Zahlensystems mit einer hinreichend langen Mantisse (und damit einem hinreichend kleinen Wert der relativen Rundungsfehlerschranke eps) der Fall ist, dann pflanzen sich im allgemeinen die einzelnen Fehler unabhängig voneinander fort. Der Gesamtfehler im Ergebnis des Algorithmus ist dann im wesentlichen gleich der Summe der Effekte der Rundungsfehler der einezelnen Schritte des Algorithmus.

In analoger Weise kann man allgemein zeigen, dass bei Vernachlässigung von Termen höherer Ordnung (der Grössenordnung eps² ,eps³ etc) für den relativen Fehler des Endresultates eines arithmetischen Algorithmus mit den Zwischenergebnissen z_i bei seiner Durchführung in einer Gleitpunktarithmetik folgende Abschätzung gilt:

falls alle Restalgorithmen zweimal differenzierbare Abbildungen darstellen. Dies bedeutet, dass der Gesamteffekt der einzelnen Rundungsfehler nicht grösser ist als die Summe der Effekte der Einzelfehler. Tatsächlich kann durch eine Kompensation von positiven und negativen Fehlern der Gesamtfehler viel kleiner sein als diese Summe (vgl. z. B. die Fehler-Nulldurchgänge). Das Vernachlässigen von Termen höherer Ordnung ist im allgemeinen gerechtfertigt, weil 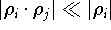gilt. die unabhängige Fortpflanzung der einzlelnen Fehler ist also meist eine realistische Beschreibung des tats&au ml;chlichen (komplexeren) Verhaltens. Wenn allerdings die Zahl der Operationen sehr gross wird, können auch Terme höherer Ordnung eine Rolle spielen. So ist z. B. in

der quadratische Term nicht mehr vernahclässigbar, sobald 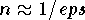gilt. Bei Verwendung einfach genauer Arithmetik tritt diese Situation bereits bei Problemen auf, die gar nicht so ausserordentlich gross sein müssen. Der übergang zu doppelt genauer Arithmetiok kann in solchen Fällen einen Genauigkeitsgewinn bei den Resultaten mit sich bringen, der weit groesser ist, als eine Verdoppelung der mantissenlänge erwarten liesse. Bei einem stabilen Algorithmus sind die Verstärkungsfaktoren 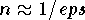nicht grösser als die Konditionszahl K des mathematischen Problems, die die Empfindlichkeit des Ergebnisses auf eine Datenänderung ausdrückt. Damit ergibt sich für einen stabilen Algorithmus mit N Einzeloperationen die grobe Abschätzung

In der Praxis überschätzt diese Schranke aber den wirklichen Fehler stark; sie könnte ja nur dann angenommen werden, wenn bei jeder Opertion tatsächlich ein relativer Rundungsfehler der Grösse eps aufträte und sich noch dazu alle diese Fälle in die gleiche Richtung, d. h. mit demselben Vorzeichen auswirkten. Auf Grund statistischer überlegungen ist bei einer zufälligen Verteilung der Vorzeichen und der Grösse eps der einzelnen relativen Rundungsfehler eher mit einem Verhalten proportional zu 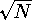und einem zusätzlichen Faktor c < 1 zu rechnen. Im Fall eines gut konditionierten mathematischen Zusammenhangs ist die Vermeidung von Auslöschungssituationen bei arithmetischen Algorithmen die wichtigste methode, um genaue Ergebnisse zu erzielen. Tatsächlich liegen jedoch nicht selten Problemstellungen vor, bei denen ein schlecht konditionierter, extrem empfindlicher Zusammenhan zwischen den Daten und dem exakten Resultat besteht. Beispiele dafür sind fast alle Aufgaben, bei denen ein sehr nahe bei Null liegendes Ergebnis aus normalgrossen Daten gewonnen wird: - Auswertung eines Polynoms P an einer Stelle x mit und 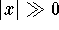, - Berechnung des Skalarproduktes zweier annähernd orthogonaler Vektoren, - Berechnung des Residuums, das sich beim Einsetzen einer Näherungslösung in ein Gleichungssystem ergibt.

Solche schlecht konditionierten Aufgaben lassen sich offenbar ohne besondere Vorkehrungen in einer Gleitpunktarithmetik nicht sinnvoll bearbeiten. Man muss entweder generell zu einer häheren Genauigkeit (einer grösseren Mantissenlänge) übergehen oder spezielle Algorithmen verwenden, die mit einer dynamischen, der Situation sich anpassenden Geanauigkeit arbeiten. Im Fall der Residuumsberechnung des obigen Beispiels werden in manchen Programmen die inneren Produkte

in doppelter Genauigkeit berechnet. Da das Produkt von zwei Gleitpunktzahlen aus 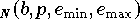stets in der Zahlenmenge 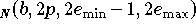liegt, tritt bei der Multiplikation kein Rundungsfehler auf, falls zwischen den einfach genauen Gleitpunktzahlen (Mantissenlänge p₁, relative Maschinengenauigkeit eps₁) und den doppelt genauen Zahlen (p₂, eps₂) tatsächlich die Beziehung p₂ > 2 p₁ gilt. 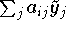Beim Aufaddieren dieser Produkte sind die relativen Additionsfehler dann durch das der doppelt genauen Gleitpunktarithmetik beschränkt, die ersten p₁ Mantissenstellen der Summe sind also im allgemeinen richtig. Die bei der abschliessenden subtraktion nach der Auslöschung an die vorderen Stellen der Mantisse rückenden Ziffern sind also - von Extremfällen abgesehen - richtig. Es gibt sogar Arithmetik-Implementierungen, bei denen die Berechnung eines Skalarprodukts eine Elementar-Operation ist, für die deshalb gilt:

Solche Implementierungen des Skalarprodukts nennt man exaktes Skalarprodukt.