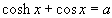 und
und 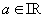
wurde auf der Basis des Newton-Verfahrens
![\[x_{n+1} = x_{n} - \frac{f(x_{n})}{f'(x_{n})}\]](pic/b07_03aj.gif)
mit

![\[\hbox{{\bf if}} \quad |x_{n} - x_{n+1}| < \varepsilon \quad
\hbox{{\bf then exit}}\]](pic/b07_05aj.gif) then exit
then exit
ein Programm geschrieben. Für a = 2, x0=1 und
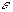 = 10-6
liefert das Programm folgende Werte als Lösung:
= 10-6
liefert das Programm folgende Werte als Lösung:
x13 = 0.0310800 bei einfach genauer Aritmetik; x32 = 0.0001307 bei doppelt genauer Aritmetik.
Wenn man die beiden Werte anschaut, merkt man den groß Unterschied zwischen den beiden Werten. Im
vorliegenden Fall sind die Komplikationen im speziellen darauf zurückzuführen, daß es
sich bei der exakten Lösung 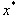 = 0 um eine mehrfache
Nullstelle der Gleichung
= 0 um eine mehrfache
Nullstelle der Gleichung 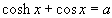 handelt.
handelt.
Man merkt es, hier kann die Variation des Toleranzparameters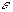 nicht verwendet werden. Für alle Werte
nicht verwendet werden. Für alle Werte
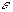 = 10-2,10-3,.....,10-8
= 10-2,10-3,.....,10-8erhält man in einfach genauer Arithmetik stets das gleiche Resultat: x13 = 0.0310800.
Beispiel (Numerische Integration): Wenn zur Lösung eines Integrationsproblems ein Integrationsprogramm eingesetzt wird, das auf Gauß-Kronrod-Formeln mit global-adaptiven Algorithmus beruht, z.B. das Programm QUADPAKqag, dann kann man die Abhängigkeit der Resultate vom Algorithmus z.B. dadurch untersuchen, daß man durch die Wahl des Parameters key verschiedene Gauß-Kronrod-Formelpaare (zwischen 7/15-Punkt-Formeln und 30/61-Punkt-Formeln) zum Einsatz bringt.
Auf jeden Fall soltte man auch die Abhängigkeit der Resultate von den Genauigkeitsparametern ( epsabs und epsrel beim Programm QUADPACK/qag) durch mindestens drei Computerläufe untersuchen: mit den ursprünglich gewälten Paramerwerten sowie Werten, die sich um die Faktoren 10 und 0.1 davon unterscheiden. Man kann aber auch durch diese Maßnahmen nicht ausschließen, daß Konstellationen auftreten, bei denen z.B. ein peak des Integranden nicht erkannt wird und denentsprechend ungenaue Resultate die Folge sind.
Bei komplexeren Aufgabenstellungen ist man in der Praxis oft nicht imstande, für einen konkreten Fall Konditionszahlen zu ermitteln. Da es jedoch für die Beurteilung der Genauigkeit einer Lösung unumgänglich ist, über die Datenfehlerempfindlichkeit Bescheid zu wissen, muß man sich diese Kenntnis auf einem anderen Weg verschaffen: durch Simulation der Störungen.
| Man ersetzt dabei den Vorgang: |
 (ein) (ein) |
| durch: |
 (viele) (viele) |
Da man im allgemeinen die exakten Daten des untersuchten Anwendungsproblems nicht kennt, ist man gezwungen, einen Datensatz (der möglichst große Ähnlichkeit mit den realen Daten hat) als "exakten" Datensatz anzusehen. Wenn möglich, sollte dies ein Datensatz sein, für den man das exakte Resultat kennt. Diesen festen Datensatz stört man nun in möglichst derselben Weise, wie es den Störeinflüssen (Meßfehler usw.) entspricht. Dies kann z.B. mit Hilfe eines Zufallszahlengenerators erfolgen, dessen Ausgangswerte eine Verteilungsfunktion besitzen, die mit jener des simulierten Störfaktors übereinstimmt. Der Zufallsgenerator kann nun dazu verwendet werden eine bestimmte Anzahl von "gestörten Datensätzen" zu generieren, die als Input für das zu untersuchende Lösungsverfahren verwendet werden. Man erhält eine Menge von Lösungen (zu einem "exakten" Datensatz), deren Variabilität Aufschlüsse über die Datenfehlerempfindlichkeit gibt. Es soll hier nicht weiter auf die statische Analyse der erhaltenen Werte eingegangen werden, es sei nur davor gewarnt, aus einer kleinen Variabilität (Streuung) auf kleine Fehler zu schließen.
Die experimentelle Sensitivitätsanalyse
ist ein sehr nützliches Hilfsmittel zur Reduktion von Unsicherheiten,
das aber auch seine Grenzen hat, vor allem dann, wenn man eine systematische
Untersuchung aller Datenvariationen in Angriff nehmen will. Wenn z.B. ein
Problem 100 skalare Eingangsdaten besitzt (z.B. die Elemente einer 10x10
Matrix) und man alle Konstellationen untersuchen will, die sich ergeben,
wenn jedes Element entweder ungestört oder um +1% oder -1% gestört
ist, dann sind hierfür 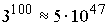 Berechnungen erforderlich. Erst mit statischen Methoden kann man in dieser
Situation eine sinnvolle Sensitivitätsanalyse durchführen, indem
man mit Hilfe eines Zufallsgenerators eine handhabbare Teilmenge aus den
3100 möglichen Datenkonstellationen auswählt und als
Berechnungseingang verwendet. Die Anzahl der durchzuführenden Berechnungen
kann man dann nach statischen Gesichtspunkten und freilich nur nach Maßgabe
des Aufwandes, den man zu investieren bereit ist, festlegen.
Berechnungen erforderlich. Erst mit statischen Methoden kann man in dieser
Situation eine sinnvolle Sensitivitätsanalyse durchführen, indem
man mit Hilfe eines Zufallsgenerators eine handhabbare Teilmenge aus den
3100 möglichen Datenkonstellationen auswählt und als
Berechnungseingang verwendet. Die Anzahl der durchzuführenden Berechnungen
kann man dann nach statischen Gesichtspunkten und freilich nur nach Maßgabe
des Aufwandes, den man zu investieren bereit ist, festlegen.
Eine Alternative zur Sensitivitätsanalyse ist die Fehleranalyse, bei der eine mathematische Untersuchung der Auswirkungen verschiedener Unsicherheitsfaktoren in qualitativer und quantitativer Form vorgenommen wird. Für einen Berechnungsvorgang können oft verschiedene Arten von Fehleranalysen vorgenommen werden, die zu verschiedenen Ergebnissen führen. So gibt es z.B. bei der Lösung linearer Gleichungssysteme verschiedene mathematische Untersuchungen und entsprechend unterschiedliche Resultate bezüglich der Auswirkung von Datenfehlern (Datenunsicherheiten) auf den Resultatvektor.
|
Die Fehleranalyse kann in mehrfacher Hinsicht Schwerigkeiten bereiten: |
| 1. Die erforderlichen mathematischen Untersuchungen könnten so kompliziert und aufwendig sein, daß eine Fehleranalyse unmöglich wird. |
| 2. Die Abschätzung der Auswirkungen der verschiedenen Unsicherheitsfaktoren kann unter Umständen so pessimistisch sein (d.h. die Auswirkungen werden so stark überschätzt), daß diese Aussagen der Fehleranalyse praktisch wertlos sind. |
| 3. Die Voraussetzungen der Fehleranalyse können so einschränkend sein, daß eine praktische Anwendung in den meisten Fällen nicht in Frage kommt; z.B. mathematische Aussagen über die Genauigkeit von Integrationsresultaten, bei denen Schranken für die höheren Abletungen der Integrandenfunktion benötigt werden, eignen sich kaum für eine praktische Fehleranalyse. |
Zusammenfassend kann gesagt werden: Weder die Sensitivitätsanalyse noch die mathematische Fehleranalyse liefern automatisierbare Möglichkeiten für die Validierung numerischer Berechnungen. Beide Techniken sind jedoch brauchbare Hilfsmittel, um den Grad der Zuverlässigkeit numerischer Berechnungen zu erhöhen. Für komplexe Problemstellungen mit hohen Zuverlässigkeitsanforderungen muß man stets auch mit einem großen Validierungsaufwand rechnen.